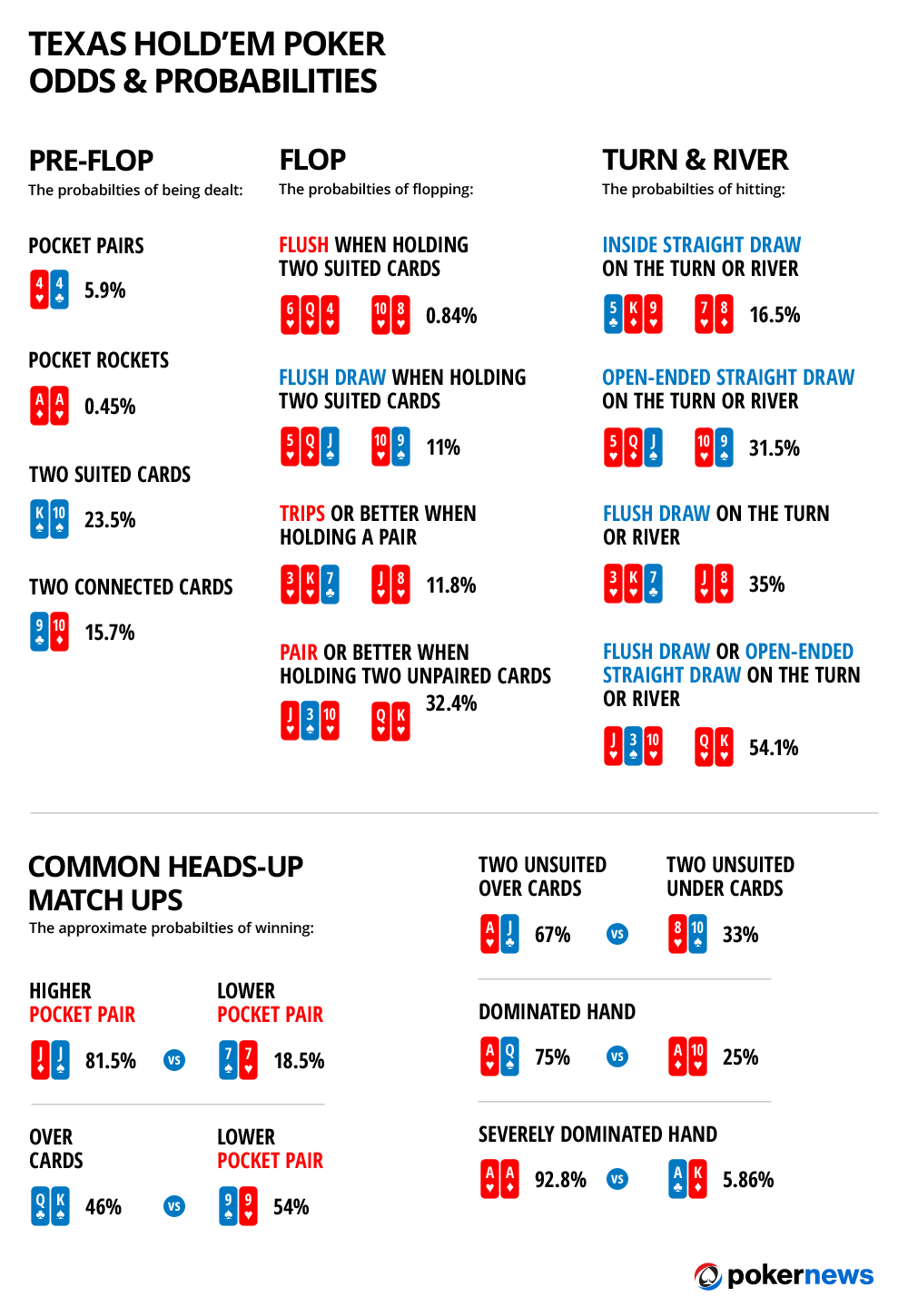
Odds Of 4 Of A Kind In Texas Holdem
Playing poker is about playing the odds. The following list gives the odds for outcomes in Texas Hold’em hands. When you realize how heavily the odds are stacked against you, you may want to rethink going all-in before the flop with two suited cards. Use the odds to your advantage: 1 percent (1-in-100): Percentage of.
The odds of hitting quads on the flop are a minuscule 0.2% or 407 to 1. By the river it goes up slightly to 2.1% but the odds are still very much against you. When you do hit four-of-a-kind you’re generally going to be the winner. Probability Of Getting 4 Of A Kind In Texas Holdem While our vetting process is very in-depth, the following summarized Probability Of Getting 4 Of A Kind In Texas Holdem elements make up the foundation of what we – and you! – should always insist upon in a Probability Of Getting 4 Of A Kind In Texas Holdem reputable USA online casino site.
Question: What is the probability of a 4 of a kind appearing on the board in texas holdem?
Solution:

- All of the following computations assume that you know only your two hole cards, and no other cards are known to you. Thus, there are 50 unknown cards after you see your hole cards.
- In the computations below, I'll use the symbol X for the card that does not fill the 4 of a kind, and an M for the cards that do fill the 4 of a kind.
- If you do not hold a pair, the probability is different than if you do hold a pair. So, we need to analyze these two cases seperately. The probability (denoted P) of getting a paired hand in the hole is 3/51=.0588235 (your first card from the deck can be any card, while the second must match it; after you get your first hole card, there are 3 cards of the 51 remaining cards that match your hole card). Thus, the probability of getting a non-paired hand is 1-.0588235=.94117647.
Case 1. Let's analyze non-paired hole cards first.
- Scenario 1: XMMMM
- Start with non-paired hole cards P=.94117647.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3 that do match X) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 6), and there are 49 cards remaining in the deck, so it has P=40/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .94117647*(50/50)*(40/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00004442.
- Scenario 2: MXMMM
- Start with non-paired hole cards P=.94117647.
- M1 can be any card not matching either of your hole cards (there are 6), and there are 50 cards remaining in the deck, so it has probability P=44/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00004495.
- Scenario 3: MMXMM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00004495.
- Scenario 4: MMMXM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00004495.
- Scenario 5: MMMMX
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00004495.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a non-pair in the hole, or P=.0002297.
Case 2. Analyze paired hole cards.
- Scenario 1: XMMMM
- Start with paired hole cards P=.05882353.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 2), and there are 49 cards remaining in the deck, so it has P=44/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .05882353*(50/50)*(44/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00000305.
- Scenario 2: MXMMM
- Start with paired hole cards P=.05882353.
- M1 can be any card not matching either of your hole cards (there are 2), and there are 50 cards remaining in the deck, so it has probability P=48/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00000307.
- Scenario 3: MMXMM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00000307.
- Scenario 4: MMMXM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00000307.
- Scenario 5: MMMMX
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00000307.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a pair in the hole, or P=.00001513.
So, now we add the two probabilities together to get the total probability of a 4 of a kind appearing on the board regardless of if your hole cards are paired or not: .0002297+.00001513=.00023955, or 4174.46 to 1.
To put this in perspective, if you played 5 days a week, 8 hours a day in a live card room at 25 hands per hour, you would see 1000 hands a week. Furthermore, IF every hand went to the river OR if you rabbit-hunted every hand and looked at all the board cards regardless of if play dictated that they be shown, you'd see a 4 of a kind on the board once a month or so. Of course, since only approximately 20% of all hands go to the river, a full-time live card room player will only see about 2 or 3 a year.
Online players generally see twice as many hands as a player in a live card room; they will see twice as many 4 of a kinds on the board than will a player that plays the same amount of time in a live poker room.
Online Play: There are manyonline sites where you can play this style of poker -- but you need to make sure that the site accepts players fom your area of residence.
- US players should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
- Players outside of the United States have additional choices, and should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
Recommended Sites: These sites have nice bonuses, great game selection, and excellent sit-and-go tournaments at all stakes. All take players from the US (as well as most non-US players, of course), and have at least a 100% initial deposit bonus for new players.
- Bovada Poker: 110% bonus!
- Americas Cardroom: 100% bonus!
- OddsMaker.com Poker: 100% bonus!
Freerolls: You can play this game for free with the chance to win real cash. Check out the online poker freeroll listings to find the date, time, and location of an upcoming freeroll.
For more information...
Good luck and have fun!
Poker can be a fun card game for the family, or a serious competitive game in which the steaks can be so enormous, even selling your house wouldn’t cover the costs.
There are many variations of poker, with Texas Hold ‘Em being the most popular worldwide.
Below are a whole bunch of poker facts and statistics which help you understand the chances of wining and the odds of getting the cards you want.
Did You Know?
A pocket pair is cards of the same rank, which means if your two cards have the same number, from 2-2 all the way up to A-A, this is called a pocket pair.
- The odds of receiving any pocket pair is 5.9% which is 16 to 1. These are also the same odds of receiving a pocket pair of 2’s.
- The odds of receiving a specific pocket pair: 0.45% or 220 to 1 These are the same odds for receiving a pocket pair of A’s.
- The odds of receiving a pocket pair of A’s twice in a row is 0.002047% or 48,840 to 1.
- The odds of receiving a pocket pair of K’s is 0.9% which is 220 to 1.
- The odds of receiving a pocket pair of Q’s is 1.4% which is 73 to 1.
- The odds of receiving a pocket pair of J’s is 1.8% which is 54 to 1.
- The odds of receiving a pocket pair of 10’s is 2.3% which is 43 to 1.
- The odds of receiving a pocket pair of 9’s is 2.7% which is 36 to 1.
- The odds of receiving a pocket pair of 8’s is 3.2 which is 31 to 1.
- The odds of receiving a pocket pair of 7’s is 3.6% which is 27 to 1.
- The odds of receiving a pocket pair of 6’s is 4.1% which is 24 to 1.
- The odds of receiving a pocket pair of 5’s is 4.5% which is 21 to 1.
- The odds of receiving a pocket pair of 4’s is 5.0% which is 19 to 1.
- The odds of receiving a pocket pair of 3’s is 5.4% which is 17 to 1.
Poker Fast Facts
The total number of possible royal flush hands in a standard 52 card deck is 4.
And the odds of making a royal flush is 649,739 to 1.

This is correct assuming that every game plays to the river.
In poker terms, the river is the name for the fifth card dealt, face-up on the board.
In total, there are 2,598,960 possible poker hands with 52 cards.
The odds of getting four of a kind in Texas Hold ‘Em is 4164 to 1.
Casinos normally change decks after 15 minutes of steady play, so that the cards can always be fresh and unmarked, as many professional players would be able to remember the certain markings on cards and use that to their advantage.
This is only a basic overview of poker odds, there are many calculators online that can help solve the odds of getting certain hands, depending on what stage of the game you’re at, what cards you currently hold and how many people are playing.
Now you are familiar with these odds, you can use them to your advantage for a better poker strategy when you finally decided to play a tournament.
Odds Of Flopping 4 Of A Kind In Texas Hold Em
In Texas Hold-Em Poker the odds of making a royal flush hand is only 649,739 to 1.